La surprenante loi de Benford
 Difficulté : débutant
Difficulté : débutant La loi de Benford est une loi mathématique et statistique, dite « loi des nombres anormaux ». Elle décrit la distribution du premier chiffres des nombres (par exemple, pour le nombre 2895, il s’agit du nombre 2). Voyons pourquoi cette loi est surprenante, et en quoi elle est utile sur les marchés financiers.
Une loi contre-intuitive
On pourrait naïvement penser aux premiers abords que, si on prend tous les nombres qui nous entourent dans la vraie vie, cette distribution est équitablement distribuée entre 1 et 9 avec une fréquence de 1/9 soit 11% pour chacun d’entre eux.
Prenons un exemple tout à fait au hasard afin de le vérifier, la population des pays les plus puissants du monde :
| Pays | Population |
|---|---|
| Etats-Unis | 334 805 000 |
| Chine | 1 448 471 000 |
| Japon | 125 585 000 |
| Allemagne | 83 809 425 |
| Inde | 1 406 632 000 |
| Royaume-Uni | 68 992 721 |
| France | 67 813 396 |
| Canada | 38 388 000 |
| Russie | 146 083 065 |
| Brésil | 215 354 000 |
On remarque que sur ces 10 exemples :
- Quatre d’entre eux commencent par le chiffre 1 (Chine, Japon, Inde et Russie)
- Un seul par le chiffre 2.
- Deux par le chiffre 3
- Puis aucun par 4 ou 5, deux par le chiffre 6, aucun par 7, un par 8 et aucun par 9.
On remarque donc une nette sur-représentation du chiffre 1 comme premier chiffre de ces nombres. Et cela n’est pas dû au hasard, c’est justement ce que cette loi démontre. Selon elle, le premier chiffre des nombre dans le monde est distribué de la manière suivante :
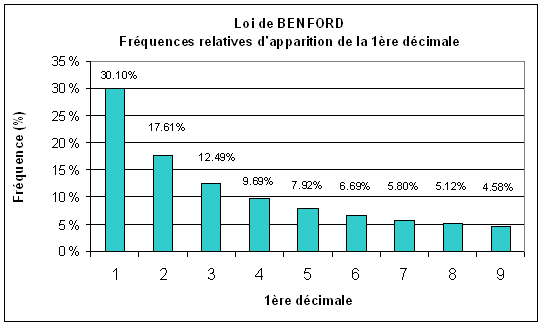
Ainsi, nous sommes ici très loin d’une distribution égale comme on pourrait légitimement s’y attendre.
Une découverte amusante
C’est au XIXeme siècle, en 1881 qu’un astronome américain, Simon Newcomb découvre cette loi par hasard. A l’époque, des livres de tables logarithmiques étaient utilisé pour les calculs, et Newcomb remarqua que les pages de logarithmes commençant par le chiffre 1 étaient bien plus usées que les autres, comme si elles étaient plus utilisées. Frank Benford fit la mêmes remarque que lui en 1938, soit plus d’un demi-siècle plus tard, et vérifiera ses conclusions sur un panel de données plus large qu’il avait à disposition (comme par exemple la longueur des fleuves, le poid des molécules). Evidemment, cette loi fut par la suite vérifiée sur les cours de bourse.
Utilisation de la loi de Benford en finance
Cette loi ne va malheureusement pas vous aider à mieux investir, mais elle a trouvé de nombreuses applications dans la détection d’anomalies, de fraudes et de manipulation des cours.
En effet, la plupart des fraudes étant basées sur la manipulation des chiffres, quelqu’un qui publiera de faux chiffres s’éloignera de cette loi naturelle. Souvent même, il fera en sorte de faire varier au maximum les chiffres qu’il génère afin qu’ils paraissent plus naturels, et ce sans penser à la loi de Benford. Malheureusement pour lui, cette volonté de les faire paraître légitimes les fera en fait s’éloigner de leur existence potentielle naturelle.
Mieux, taper au hasard des chiffres sur un pavé numérique donnera une toute autre distribution de par la forme même de ce pavé, avec une distribution cette fois centrée sur le chiffre 5 comme sur le schéma ci-dessous :
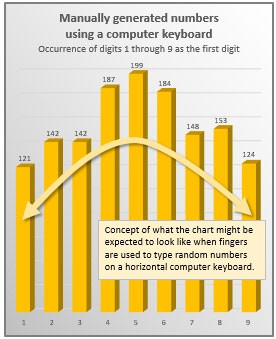
Si ces chiffres sont cette fois générés par un algorithme, leur distribution aura toutes les chances de ressembler à la suivante :
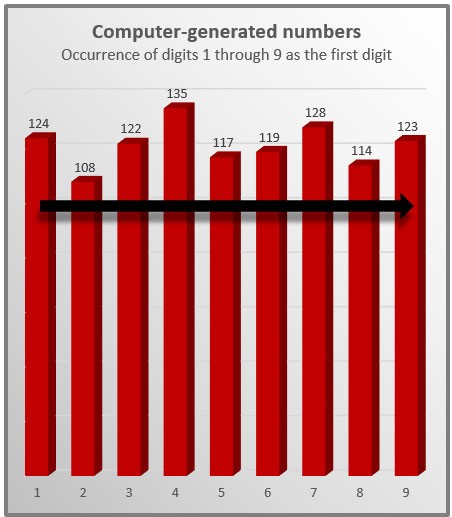
Comme on peut le constater, leur détection en utilisant la loi de Benford est assez aisée. D’ailleurs, après la faillite d’Enron en 2001, des études ont réalisé que la fraude aurait été trouvable en appliquant simplement cette loi sur leurs publications.
Alors bien évidemment, il est possible de générer de faux nombres suivant cette loi, et donc plus difficilement détectables. Cette loi est donc un outil parmi d’autres de détection des fraudes comptables, mais qui a de nombreuses fois montré ses preuves dans l’histoire.